Pour aller plus loin:
vous trouverez une liste de documents présentant plus amplement le modèle logistique en cliquant sur le lien suivant:
~~~~~~~~~~~~~~~~~~~~~~

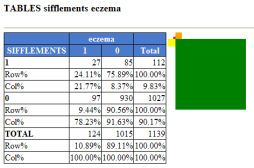
Le tableau 2X2, obtenu avec la commande "TABLES", donne le dénombrement de l'échantillon en fonction de l'eczéma (le symptôme) et les sifflements (l'exposition) :
27 sujets malades et exposés;
97 sujets maldes non exposés;
85 sujetes non malades et exposés;
1015 sujets non malades et non exposés.
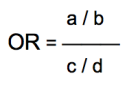
La force et le sens de l'association entre la maladie et l'exposition est mesurée par l'Odds Ratio qui est le rapport entre le rapport des sujets malades sur les non malades parmi les sujets exposés (a/b) et le rapport des sujets malades sur les non malades parmi les sujets non exposés (c/d):
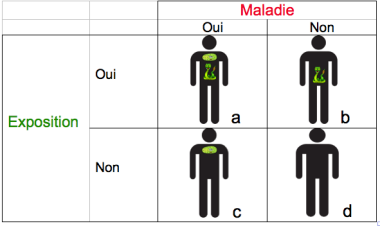
Le résultat du dénombrement peut se présenter sous forme d'un tableau 2X2, croisant la maladie et l'exposition:
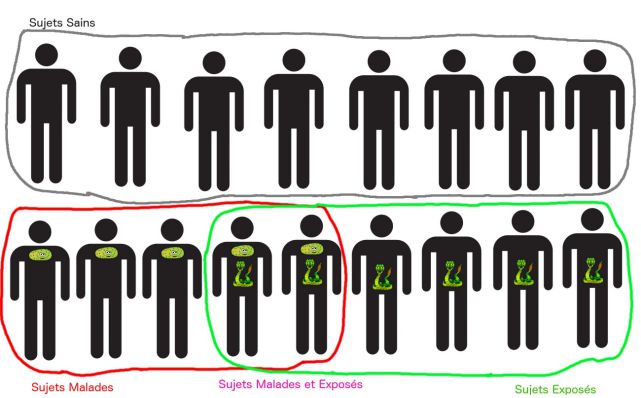
Dans le cas de l'étude de la relation entre une maladie et un facteur d'exposition (codé en oui/non), l'échantillon issu de la population de l'étude est dénombré en fonction de la présence de la maladie, et de l'exposition au facteur considéré:
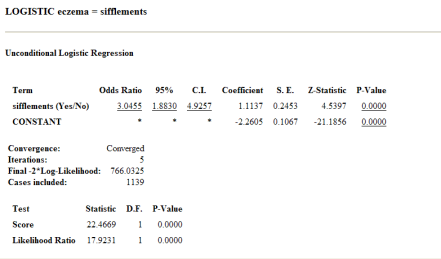
Dans la fenêtre résultat de la commande "Régression Logistique", on lit la valeur de l'OR, ici 3,05 en arrondisant, et son intervalle de confiance à 95 % à côté, ainsi que la valeur p, ici inférieure à 0,0001.
On peut donc dire que les enfants qui ont des sifflements dans la poitrine ont une probabilité plus grande d'avoir de l'eczéma que ceux qui ne présentent pas de symptômes de sifflements, car la valeur de l'OR de 3,05 est très significativement supérieure à 1 (en effet son l'intervalle de confiance n'inclut pas 1, et la valeur p est très inférieure à 0,05).
Les valeurs p qui apparaissent en bas (p est inférieur à 0,0001) correspondent au degrés de signification du modèle logistique global (avec toutes les variables explicatives). Ici comme il n'y a qu'une seule variable explicative (les sifflements) ces valeurs de p sont proches de celle associée à la variable sifflements, et indiquent que le modèle est statistiquement très significatif.
Association estimée par Epi Info exprimée par l'Odds Ratio


Facteur de Risque
(variable explicative, indépendante)
Maladie ou Symptômes
(variable à expliquer, dépendante)


Exemple dans une étude sur l'allergie chez les enfants.
Variable symptôme à expliquer: "avoir de l'eczéma"
Variable facteur d'exposition : "avoir des sifflements".
Le modèle logistique calculera la probabilité d'avoir de l'eczéma chez les enfants avec des sifflements, et la probabilité d'avoir de l'eczéma chez les enfants ne présentant pas de sifflement, puis l'Odds Ratio correspondant.
Sorties des résultat obtenus avec Epi Info:
Le Principe de la Régression Logistique
Lorsque l’on veut étudier la relation entre une variable binaire (qualitative à deux modalités) et d’autre variables qualitatives ou quantitatives, on utilise une régression logistique.
En épidémiologie la variable binaire d’intérêt, la variable à expliquer, (aussi appelée variable dépendante) est souvent la mesure de l’absence ou la présence d’une maladie ou d’un symptôme, et on s’intéresse à la fréquence de la maladie.
Le modèle logistique permet de calculer la probabilité de la caractéristique étudiée (souvent la présence d'une maladie), suivant les valeurs de variables explicatives dites aussi variables indépendantes.
L’intérêt de ce modèle est qu’il permet d’estimer l'association entre la maladie (la variable dépendante dichotomique) et un facteur d’exposition (la variable explicative) sous forme d’Odds Ratio,
et la fonction logistique utilisée pour la modélisation a une forme sigmoïde qui correspond à une forme de relation souvent observée entre une dose x et la fréquence d’une maladie y.
Article publié le 24 novembre 2017

Introduction au modèle logistique :
Le modèle de régression logistique est très utilisé en épidémiologie.
Cette série d'articles aborde d'abord le principe du modèle de régression logistique, puis son utilisation dans Epi Info avec des exemples pratiques de calculs.
La régression à une seule variable, puis la régression avec plusieurs variables. Enfin est abordé le cas particulier des variables nominales.

La Régression Logistique dans Epi Info 7 (1/5)

