On retrouve bien la forme sigmoïde de la courbe représentant la probabilité d'avoir une maladie cardiaque en fonction de l'âge, cette probabilité augmentant avec l'âge.
Il est à noté cependant, que dans notre échantillon de patients, l'âge minimum était de 29 ans, et l'âge maximum de 77 ans (limites marquées par les droites en pointillées), et que donc la modélisation de cette courbe n'a été réalisée qu'avec des données de patients entre ces deux âges, mais pour bien voir la forme de cette courbe, on a extrapolé les résultats à des âges inférieurs à 29 ans et supérieurs à 77 ans.

Remarque:
le modèle logistique modélisant la relation entre la probabilité d'être malade (dans notre exemple d'avoir une maladie cardiaque) en fonction d'un facteur de risque, ici l'âge des patients, à partir des résultats du modèle (les coefficients qui apparaissent dans la colonne "Coefficient"), on peut calculer cette probabilité.
Dans notre exemple cela donne la coube suivante:
~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~
Les valeurs p qui apparaissent en bas (encadrées en bleue, p est < 0,0001) correspondent au degrés de signification du modèle logistique global (avec toutes les variables explicatives). Ici comme il n'y a qu'une seule variable explicative (le sexe) ces valeurs de p sont proches de celle associée à la variable sexe, et indiquent que le modèle est statistiquement significatif.
Dans la fenêtre résultat, on lit la valeur de l'OR, ici 1,05 en arrondissant, et son intervalle de confiance à 95 % à côté (entourés en rouge 1,03 - 1,08), ainsi que la valeur p, ici 0,0016 (entourée en vert).
b) En reprenant la formule de calcul de l'Odds Ratio, avec les nombres de sujets qui apparaissent dans le tableau 2X2 croisant la variable sexe avec la variable diagnostic de maladie cardiaque, on peut retrouver la valeur de l'OR:
* le numérateur de l'OR correspond au rapport des sujets avec une maladie cardiaque sur ceux qui ne l'ont pas parmi les patients hommes (codé 1) soit:
114 / 92 = 1,239
* le dénominateur de l'OR correspond au rapport des sujets avec une maladie cardiaque sur ceux qui ne l'ont pas parmi les patients femmes (codé 0) soit:
25 / 72 = 0,347
L'Odds Ratio correspond au rapport entre ces deux rapports, soit:
1,239 / 0,347 = 3,57
Dans l'échantillon d'étude, le diagnostic de maladie cardiaque est donc significativement lié à l'âge, la valeur de l'OR étant significativement supérieure à un. Plus les patients sont âgés, plus la probabilité d'avoir un diagnostic de maladie cardiaque est grand.
Remarques :
a) Les valeurs de l'Odds Ratio calculées par le modèle logistique sont les mêmes que celles obtenues avec la commande TABLES, car ici le modèle logistique ne tient compte que d'une seule variable explicative:

Les résultats de la régression logistique apparaissent alors dans la fenêtre de sortie:

☞ Dans la fenêtre de la commande Régression Logistique, après avoir d'abord sélectionné la variable à expliquer dans le champ en haut à gauche "Variable à Expliquer", ici la variable "Maladiecard", on sélectionne la variable explicative, dans le champ nommé "Autres Variables" au milieu en haut, ici la variable "Age".
On clique enfin sur le bouton OK pour lancer le calcul.
1.2 La régression logistique simple avec une variable explicative quantitative
Dans la fenêtre résultat, on lit la valeur de l'OR, ici 1,15 en arrondissant, et son intervalle de confiance à 95 % à côté (entourés en rouge), ainsi que la valeur p, ici 0,66 (entourée en vert).
Avec l'hyperglycémie, l'association n'est pas statistiquement significative, car l'intervalle de confiance à 95 % de la valeur de l'OR des hommes (codés 1 dans la variable Sexe) sur les femmes (codées 0) inclut 1, et la valeur p est supérieure à 0,05.

Les résultats de la régression logistique apparaissent alors dans la fenêtre de sortie:


☞ Cette fois, dans la fenêtre de la Régression Logistique, après avoir d'abord sélectionné la variable à expliquer dans le champ en haut à gauche "Variable à Expliquer", ici la variable "Maladiecard", on sélectionne la variable explicative, dans le champ nommé "Autres Variables" au milieu en haut, ici la variable "Glycémie".
On clique enfin sur le bouton OK pour lancer le calcul.
B) Association entre le diagnostic de maladie cardiaque et l'hyperglycémie des patients

Dans la fenêtre résultat, on lit la valeur de l'OR, ici 3,57 en arrondissant, et son intervalle de confiance à 95 % à côté (entourés en rouge), ainsi que la valeur p, ici <0,0001 (entourée en vert).
On peut donc dire que, dans notre échantillon d'étude, les hommes ont une probabilité plus grande d'avoir un diagnostic de maladie cardiaque que les femmes, car la valeur de l'OR des hommes (codés 1 dans la variable Sexe) sur les femmes (codées 0) est significativement supérieure à 1 (en effet son l'intervalle de confiance à 95 % n'inclut pas 1, et la valeur p est inférieure à 0,05).

Les résultats de la régression logistique apparaissent alors dans la fenêtre de sortie:

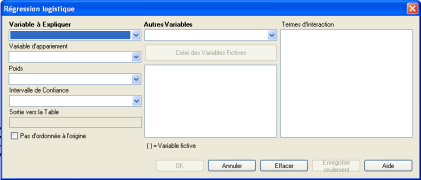
☞ Dans la fenêtre de la Régression Logistique qui apparaît, il faut d'abord sélectionner la variable à expliquer dans le champ en haut à gauche "Variable à Expliquer", ici la variable "MaladieCard", puis sélectionner la variable explicative, dans le champ nommé "Autres Variables" au milieu en haut, ici la variable "Sexe".
On clique enfin sur le bouton OK pour lancer le calcul.
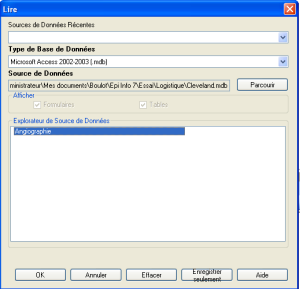
A partir du module d'Analyse des Données Classique, on doit d'abord lire la table de données de notre exemple (projet "Cleveland.mdb", table "Angiographie")

Pour illustrer l'utilisation de cette commande, prenons l'exemple d'une enquête sur des personnes allant à l'hôpital pour y subir une angiographie.
Le résultat de cet examen est le diagnostic d'une maladie cardiaque.
On veut à partir des données de l'enquête estimer, séparément, les associations entre ce diagnostic et le sexe des patients, leur hyperglycémie à jeun (> 120 mg/dl).
Le diagnostic de maladie cardiaque est notre variable de résultat, notre variable à expliquer.
Le sexe des patients est une de nos variable explicative (qualitative à 2 modalités) ou variable d'exposition.
L'hyperglycémie des patients est une autre de nos variables explicatives (qualitative à 2 modalités) ou variable d'exposition.
Enfin, l'âge des patients est une notre dernière variable explicative, mais cette fois quantitative (variable continue, cf. l'annexe sur les types de variable).
On a donc:
!!! Attention !
Epi Info n'accepte comme
variable de résultat
(la variable dichotomique à expliquer) que les
variables numériques codées en
0/1
, ou
les variables de type
Oui/Non
(Yes/no).
Si ce n'est pas le cas, vous devrez créer une nouvelle variable en transcodant la variable d'origine avec les commandes Epi Info du module d'analyse
DEFINIR
et
TRANSCODER
.
1.1 La régression logistique simple avec une variable explicative qualitative à 2 modalités
A) Association entre le diagnostic de maladie cardiaque et le sexe des patients
Note et remarque au sujet des données:
Les données de cet exemple sont tirées d'une vraie enquête réalisée dans une clinique de Cleveland aux Etats Unis d'Amérique, au près de 303 patients, en 1988.
Ces données ont été recueillies sous la direction de Robert Detrano, M.D., Ph.D, au V.A. Medical Center, Long Beach and Cleveland Clinic Foundation.
J'utilise ces données à des fins pédagogiques pour montrer un exemple de régression logistique, mais à l'origine, elles n'ont pas été collectées pour cela. Les résultats rapportés ici ne sont pas à prendre en compte en tant que de réelles analyses épidémiologiques, ils ne servent qu'à illustrer la régression logistique sous Epi Info.
☞ Pour calculer le modèle logistique, on utilise la commande REGRESSION LOGISTIQUE qui se trouve dans le groupe des commandes "Statistiques Avancées".
Facteur de Risque
(variable explicative, indépendante)
sexe
âge
hyperglycémie
Maladie ou Symptômes
(variable à expliquer, dépendante):
diagnostic de maladie cardiaque


Article publié le 24 janvier 2018

1. La Régression Logistique Simple avec Epi Info 7:
Dans le module d'Analyse des Données d'Epi Info, le modèle logistique peut être appliqué à partir de la commande REGRESSION LOGISTIQUE.
Dans le cas de la régression logistique simple, on teste l'association entre une variable dépendante de type oui/non (comme une maladie), et une variable indépendante (si elle est aussi dichotomique, on parle de variable d'exposition).
Sommaire
1. La Régression Logistique Simple.

La Régression Logistique dans Epi Info 7 (2/5)

