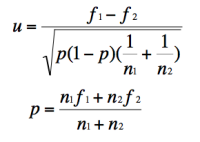
On obtient une probabilité exacte de plus de 0,10 (p-value), donc on ne rejette pas l'hypothèse nulle au seuil 0,05, et on conclut que ce service a une fréquence d'exposition aux solvants comparable à celui de l'ensemble de l'hôpital.

2: Test binomial exact
Exemple: dans un échantillon de 20 personnes sélectionnées au hasard dans un service donné d'un hôpital, 6 sont exposées à des solvants. Dans l'ensemble des services de cet hôpital la fréquence de l'exposition à ces solvants est de 0,15.
Est-ce que le service étudié à un pourcentage d'exposition au solvant comparable à celui de l'ensemble de l'hôpital ?
La taille de notre échantillon étant inférieur à 30, on effectue un test binomial exact avec R en utilisant la fonction binom.test(), avec pour arguments 6, le nombre de personnes exposées, 20 la taille de notre échantillon, et 0,15, la fréquence théorique de l’exposition étudiée.
On obtient pobs = 0,37 soit une valeur bien supérieure à 0,05, valeur seuil souvent retenue.
Donc on ne rejette pas l'hypothèse nulle, et on en conclut que la fréquence de l'anomalie est comparable à celle de la France entière.
1: Calcul de la statistique U
Prenons comme exemple, en France (population de référence) une anomalie génétique apparaissant avec une fréquence de p0=0,001.
Dans une région on trouve 7 anomalies parmi n=5000 naissances, soit une fréquence observée f=7/5000=0,0014.
La fréquence de cette anomalie dans la région est-elle comparable à celle de la France entière ?
On calcule pour cela la statistique U, car n est grand, et le nombre d'anomalies est supérieure à 5.
Voilà comment on procède avec R en utilisant la fonction pnorm() qui donne la valeur de la fonction de distribution de la loi normale centrée réduite:
on calcule d'abord la statistique U, puis la probabilité critique pobs que le u observé ait la valeur obtenue si l'hypothèse nulle est vraie.
Fiche récapitulative :
Article publié le 1er Octobre 2014


Syntaxe des tests avec le logiciel R.
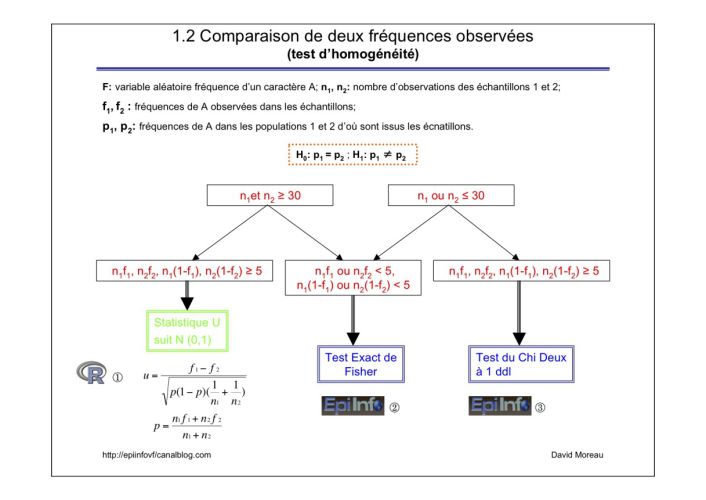
2. Si, quelle que soit la taille des échantillons n1 et n2, le nombre d'individus avec le caractère A dans un des échantillons est de moins de 5 (n1f1 ou n2f2 < 5), ou si le nombre d'individus ne présentant pas le caractère A dans un des échantillons est de moins de 5 ( n1(1-f1) ou n2(1-f2) < 5 ),
alors on effectue un test exact de Fisher.
Problématique:
On étudie un caractère donné noté A (être malade, être exposé à un facteur de risque de maladie, avoir un symptôme…) dans deux populations d'individus notées G1 et G2.
On observe :
f1, la fréquence de la présence de A dans un échantillon d'individus de taille n1 tiré de la population G1;
f2, la fréquence de la présence de A dans un échantillon d'individus de taille n2 tiré de la population G2.
La question est de savoir si les fréquences de A de chaque population G1 et G2, notées p1 et p2 sont égales (c'est l'hypothèse nulle H0 pour un test bilatéral) ou sont statistiquement différentes (c'est l'hypothèse alternative H1), en comparant les fréquences observées f1 et f2.
C'est ce que l'on appelle un test d'homogénéité.
Tests à réaliser :
1. Si la taille des échantillons est plus grand que 30 individus (n1 et n2 ≥ 30) et si le nombre d'individus avec le caractère A dans chaque échantillon est de plus de 5 (n1f1 et n2f2 ≥ 5), ainsi que le nombre d'individus ne présentant pas le caractère A ( n1(1-f1) et n2(1-f2) ≥5 ),
alors on peut calculer la statistique U (correspondant à la différence entre les fréquences observées) qui, sous l'hypothèse nulle, suit une loi normale centrée réduite N (0,1) :
Les tests statistiques de comparaison:
1.2 Comparaison de deux fréquences observées

